Line Drawing Algorithms

Introduction A pixel display space cannot represent real world phenomena exactly. The digitising process can only produce an approximation of the analogue world. If the pixel size is such that the eye cannot distinguish adjacent pixels the problem is less apparent, but nevertheless it is necessary to provide a visualisation of objects as accurately as possible, such that the eye is given the information required, albeit an approximation. Figure 1 gives an example of a pixel display representing a horizontal line and a diagonal line.

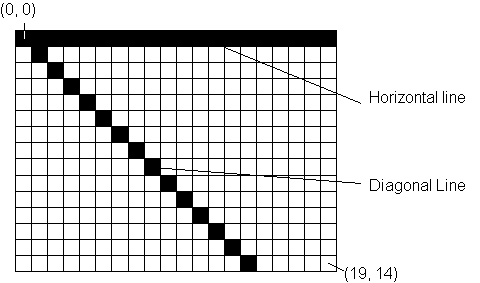
Figure 1.

The lines follow the required path, but their characteristics are different. The horizontal line has a constant width along its length. The diagonal line has a width which varies between 0 and 1.414 pixel units along its length. The average width of this line is 0.707. The eye would perceive the diagonal line as being narrower than the horizontal line. In perceptual terms a line should

• appear to have a constant width along its length
• appear to have a constant width independent of the direction the line
• start and end at the correct points (co-ordinates)
• follow a path as close as possible to that of the ideal straight line

From the point of view of hardware and software a line should be efficient to implement and therefore should

• only compute the minimum number of pixels to draw the line effectively
• only use integer arithmetic (real arithmetic is slower to compute)
• only use addition, subtraction and shift (multiply and divide are slower to compute)

Figure 2 shows an ideal line accompanied by its pixel representation.

When implementing a line drawing algorithm all the points above must be taken into account. Fundamental graphics algorithms, however, are different in that their implementation may not just be in software, but may also be in hardware. This means the algorithm has to be capable of incorporation into a digital electronic circuit.

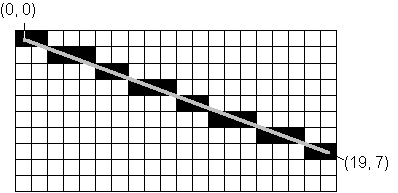
Figure 2.

There is also a compromise between the requirements in the real world and those limitations posed by hardware. For example, a line may need to start at a co-ordinate with a screen equivalent of (3.74, 2.89) and end on the co-ordinate (135.8, 77.98). Since pixels only exist on integer co-ordinates there has to be some compromise in the start and end positions.

For the remainder of this discussion we will assume that we wish to implement a procedure for drawing a straight line of unit width with integral start and end co-ordinates. The declaration for this would be:

 PROCEDURE DrawLine(X1, Y1, X2, Y2: Integer);

We will also assume that we have available a function capable of plotting an individual pixel (for example the PutPixel procedure in Borland Pascal).

Simple DDA The simplest algorithm for drawing a line is based round the mathematical description for points on a straight line. It breaks down a straight line into a set of equally spaced points. Figure 3 shows the basic principle.

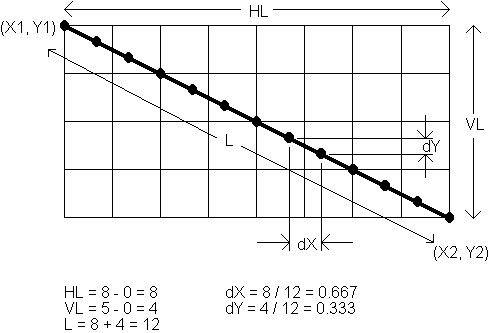
Figure 3.

The horizontal length of the line is given by:

 
 HL = X2 - X1

The vertical length of the line is:

 
 VL = Y2 - Y1

The real length of the line is SQRT(SQR(HL)+SQR(VL)) but to save calculation an estimate of the line length could be:

 
  L = ABS(HL) + ABS(VL)

If we divide the line up into L equal sections then each section will have a horizontal length of dX = HL/L and a vertical length of dY = VL/L. So if we start from (X1, Y1) each successive point along the line will be (dX, dY) further along. We can then draw a pixel at the nearest position to each point.

Figure 4 gives the Pascal code for this algorithm.

 
 PROCEDURE DrawLine(X1, Y1, X2, Y2: Integer);
 VAR
 HL, VL, L: Integer;
 dX, dY, X, Y: Real;
  Count: Integer;
 BEGIN
  HL := X2 - X1;
  VL := Y2 - Y1;
 L := Abs(HL) + Abs(VL);
 dX := HL / L;
 dY := VL / L;
 X := X1;
 Y := Y1;
 FOR Count := 0 TO L DO
 BEGIN
 PutPixel(Round(X), Round(Y), White);
 X := X + dX;
 Y := Y + dY
 END
 END;

Figure 4.

This algorithm has several deficiencies. It actually computes more points than pixels. This means the same pixel can be plotted more than once, or even worse the pixels may be bunched and give an uneven line width. The algorithm also uses real arithmetic and divisions. If you try this procedure and compare it in speed with the Borland Pascal Line procedure you will see that it is very slow.

---

Bresenham's Line Drawing Algorithm
Bresenham describes an algorithm which in its initial form attempts to implement a line which adheres to the perceptual criteria, and ignores the efficiency aspect. However, the modified version of the algorithm in the following section is optimised completely.

The basic algorithm describes how a line may be drawn in the octant between 0 degrees and 45 degrees. The algorithm can be implemented for each octant and thus covers all possible lines.

(Note that horizontal, vertical and diagonal lines are ignored as these are trivial cases and can be drawn directly with no computation.)

e.g. DrawLine(3, 4, 12, 13) is:

 
 FOR I := 0 TO 9 DO
  PutPixel(X1 + I, Y1 + I)

Bresenham's algorithm proposes that each successive pixel must be across by one pixel, but may or may not move down one pixel. The decision as to whether to move down one pixel is made by determining which position has the smallest error. The slope of the actual line (dy/dx) determines how far the actual line moves down the screen as we move across one pixel at a time. By comparing the actual line position with the current pixel we can check whether to move down one pixel or not. Figure 5 shows this is diagrammatic form.

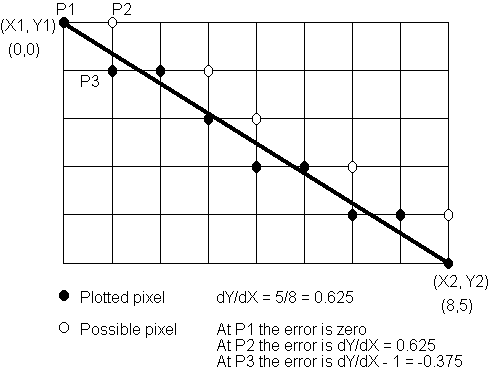
Figure 5.

If the y co-ordinate does not change, the error will always increase by dy/dx as you move along the line. At some point the error will become greater than 0.5 and so the line should be drawn with a pixel 1 row down the screen. In this case the error will reduce by one. Figure 6 gives the Pascal code for this algorithm.

 
 PROCEDURE DrawLine(X1, Y1, X2, Y2: Integer);
 VAR
 Error, DYbyDX: Real;
 Count: Integer;
  BEGIN
  DYbyDX := (Y2 - Y1)/(X2 - X1);
  Error := 0;
 FOR Count := X1 TO X2 DO
 BEGIN
 PutPixel(Count, Y1, White);
 Error := Error + DYbyDX;
 IF Error > 0.5 THEN
 BEGIN
 Y1 := Y1 + 1;
 Error := Error - 1
 END
 END
 END;

Figure 6.

As you can see there is still real arithmetic and a division, but the co-ordinates are calculated as integers. The algorithm is an improvement, but work needs to be done to make it more efficient. The following section shows how this can be done.

---

Bresenham's Modified Line Drawing Algorithm
Bresenham's algorithm only uses real arithmetic to calculate the error term. The error term is only actually used in a comparison. The modified algorithm uses a mathematical rule which states that:

 
 if a > b and c > 0
 then a*c > b*c

If we look at the comparison term in the algorithm we see

 
 error > 0.5

both sides are real numbers. If we multiply both sides by 2 the comparison is still valid, but the right hand side is now an integer.

 
i.e. 2*error > 1

The error term is calculated by adding the dY/dX term. If we scale both sides of the comparison by dX we end up with integers on both sides of the comparison.

 
 i.e. 2*dX*error > dX

If we start the algorithm by setting the error to -dX, the comparison is made more simple. We can compare to zero.

 
 i.e. 2*dX*error - dX > 0

The same effect can be obtained by performing all calculations with previously scaled values, rather than calculate 2*dX*error at each stage. The end result is the code given in Figure 7

 
 PROCEDURE DrawLine(X1, Y1, X2, Y2: Integer);
 VAR
  Error, DXtimes2, DYtimes2: Integer;
  Count: Integer;
 BEGIN
 DYtimes2 := (Y2 - Y1) SHL 1;
 DXtimes2 := (X2 - X1) SHL 1;
 Error := X1 - X2;
 FOR Count := X1 TO X2 DO
 BEGIN
 PutPixel(Count, Y1, White);
 Error := Error + DYtimes2;
 IF Error > 0 THEN
 BEGIN
 Y1 := Y1 + 1;
 Error := Error - DXtimes2
 END
 END
  END;

Figure 7.

Exercises

• Dowload the demonstration program and examine it to see how it works for all eight octants. The program is written in Pascal using Delphi. Load the example into Delphi and see how Delphi makes it possible to implement graphical algorithms involving pixel drawing. Check out the link to the Pascal for Delphi Tutorial if your Pascal is rusty.
• Using the demonstration program as a starting point try to modify it to use the simple DDA algrothm. How might you test which is the fastest algorthm?

---

 
Copyright (C) 1995, 1996




**************************
 
***********************

---